1.3.1 Digitale kretser
Den digitale elektroniske utviklingen har gått fra logiske porter til dagens mikroprosessorer. Oppfinnelsen av mikroprosessoren var en naturlig følge av en utvikling som begynte med den integrerte, digitale kretsteknologien. Før dette var den digitale teknologien basert på diskrete komponenter (resistanser, dioder, transistorer etc.) og elektromekaniske komponenter (releer, kontakter etc.).
De logiske portene kan kombineres i nært sagt et uendelig antall ulike kombinasjoner og kalles derfor også for kombinatoriske kretser. Logiske nettverk kan benyttes til å løse større logiske operasjoner og funksjoner. Siden de består av en kombinasjon av logiske porter, kalles de også kombinatoriske nett. Større kombinatoriske nett lar seg ofte forenkle og bearbeide ved hjelp av logiske regneregler (boolsk algebra).
Ved hjelp av logiske porter kan vi bygge vipper. Disse kan videre brukes til bygging av tellere, registre, regnekretser og datalager som er basis for datateknologi og datamaskiner.
1.3.1.1. Fra logiske porter til mikroprosessorer
Den digitale elektroniske utviklingen har gått fra logiske porter til dagens mikroprosessorer. Oppfinnelsen av mikroprosessoren var en naturlig følge av en utvikling som begynte med den integrerte digitale kretsteknologien. Før dette var den digitale teknologien basert på diskrete komponenter (resistanser, dioder, transistorer etc.) og elektromekaniske komponenter (releer, kontakter etc.).
Ved hjelp av logiske porter kan vi bygge vipper. Disse kan videre brukes til å bygge tellere, registre, regnekretser og datalager som er basis for datateknologi og datamaskiner.
Logiske porter og kombinatoriske nett
Som vi ser, danner de logiske portene grunnlaget for dagens datateknologi. Hver enkelt port er bygget opp av transistorer, TTL-kretsene (Transistor–Transistor Logic) av bipolare transistorer og CMOS (Complementary Metal Oxide Semi-conductors) av MOS-transistorer. De logiske portene kan kombineres i nær sagt et uendelig antall ulike kombinasjoner og kalles derfor også for kombinatoriske kretser.
Kombinatoriske nett
Logiske nettverk kan benyttes til å løse større logiske operasjoner og funksjoner. Siden de består av en kombinasjon av logiske porter, kalles de også kombinatoriske nett. Større kombinatoriske nett lar seg ofte forenkle ved hjelp av logiske regneregler (boolsk algebra).
De digitale kretsene skal ofte drive eller styre strømkrevende komponenter som releer, motorer etc, Kretsene leverer ikke særlig mye strøm, og spenningene er lave. Signalene må derfor forsterkes, noe vi kan gjøre med såkalte driverkretser, også kalt bufferkretser.
PLD-kretser
PLD er en forkortelse for Programable Logic Device og er en samlebetegnelse for forskjellige typer integrerte programmerbare logiske kretser for konstruksjon av logiske og sekvensielle nettverk. Programmering av PLD-kretser foregår etter samme prinsipper som programmering av PROM-minnebrikker. Kretsene er rimelige i innkjøp sammenlignet med tilsvarende antall porter med konvensjonelle portkretser, men krever til gjengjeld spesielt utstyr for selve programmeringen. Med PLD oppnår vi høy pakketetthet, som igjen resulterer i et langt lavere effektforbruk enn tilsvarende kretsløsninger med bruk av konvensjonelle TTL- eller CMOS-kretser. Flere logiske nett kan også samles på samme brikke. Noen typer PLD er slettbare og lar seg reprogrammere. Programmeringen foregår med en egen programmeringsenhet som tilkobles PC. Ut fra et logisk uttrykk kan PLD-kretsen programmeres, så hvis dette uttrykket er kjent, blir programmeringen relativt enkel. At PLD-kretsene er programmerbare, er selvsagt viktig å være klar over under eksempelvis feilsøking og reparasjon. Har vi mistanke om at feilen ligger i PLD-en, er det ikke bare å skifte komponenten med en av samme betegnelse. Vi må i tillegg ha adgang til komponentens programmerte innhold og det programmeringsverktøyet som trengs.
ASIC-kretser
ASIC-kretser (Application Spesific IC) er en form for programmerbare kretser der innholdet er spesifisert av en bruker, og kretsen blir spesialkonstruert på bestilling hos en produsent som eksempelvis Motorola, Texas Instruments eller Philips. ASIC er aktuelt når det er snakk om store kvanta av én og samme krets. Sett fra brukerens side kan PLD være mer anvendelig siden de kan programmeres på stedet dersom man har utstyr for det.
Logiske funksjoner
I dagliglivet er vi vant med å trekke logiske slutninger og gjøre valg ut fra forutsetninger, informasjon og impulser. Samme tankegang ligger egentlig til grunn for den logiske digitale teknologien. Vi kan ta for oss et eksempel:
Kari og Ola har planlagt en fisketur, men dersom fisketuren skal bli realisert, må følgende to forutsetninger være til stede: Det må være bra vær, og båten må være i orden. Dersom begge disse betingelsene er oppfylt, blir det fisketur. Hvis vi nå kaller bra vær for A, ok båt for B og fisketur F, kan vi uttrykke dette som
F = A og B
Vi har uttrykt en logisk funksjon, i dette tilfellet en OG-funksjon. På samme måte uttrykkes logiske funksjoner digitalteknisk, men i stedet for å skrive og, bruker vi en prikk og uttrykker dette som
F = A ∙ B eller bare F = A B
Selvsagt kunne vi lagt inn flere betingelser, som for eksempel at fiskeutstyret må være i orden, og kalt denne for C. Da vil vi få
F = ABC
OG-funksjon
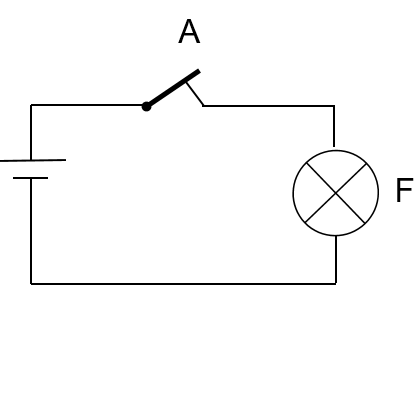
Lukkekontakter i serie danner en OG-funksjon.
F = A og B
F = A ∙ B
Dersom både kontakt A og kontakt B lukkes, vil lampa F lyse, altså en OG-funksjon.
Eller-funksjon
Lukkekontakter i parallell danner en ELLER-funksjon.
F = A eller B
F = A + B
Dersom kontakt A eller kontakt B lukkes, vil lampa F lyse, altså en ELLER-funksjon. Symbolet + brukes for å utrykke en ELLER-funksjon.
Ikke-funksjon
En brytekontakt utgjør en IKKE-funksjon.
F er lik A invertert. Dette uttrykkes som:
F = A (med strek over)
Logiske porter
Logiske porter kan betraktes som byggeklosser i all digital elektronikk, fra enklere digitale styrekretser til mikroprosessorer og datamaskiner, og kalles derfor logiske grunnelementer.
De tre grunnelementene tegnet som logiske elementer (europeiske og amerikanske tegningssymboler) og lukke- og brytekontakter samt engelske symbolnavn som vi vanligvis finner i datablad:
Europeiske og amerikanske symboler for logiske porter
NOG- og NELLER-port
Ved å kombinere en OG-port og en IKKE-port får vi en NOG-port (eng.: NAND):
Ved å kombinere en ELLER-port og en IKKE-port får vi en NELLER-port (eng.: NOR):
Digitale byggeklosser
Som vi har sett, kan de logiske funksjonene realiseres ved eksempelvis elektriske kontakter/brytere. Dette ble også gjort i de første regnemaskinene, der man benyttet relékontakter og elektromekaniske brytere.
Etter hvert som elektronikken (dioder og transistorer) vant terreng, realiserte man disse funksjonene ved hjelp av elektroniske kontakter og brytere. Men for å få disse til å virke og ikke minst kobles sammen til større logiske funksjoner, måtte man i stor utstrekning tenke elektroniske strømmer og spenninger og gjøre innviklede elektrotekniske beregninger.
Det var derfor et stort fremskritt da man begynte å bygge de logiske funksjonene inn i integrerte kretser, eller såkalte IC-er (Integrated Circuits), som logiske porter.
Kretsene ble standardisert med standard inngangsstrømmer og spenninger og likeledes for utgangene. Dette har gjort det enklere å sette sammen enkeltelementer til større logiske nettverk.
Sannhetstabell
Vi har sett at logiske funksjoner kan verifiseres ved hjelp av logiske uttrykk. De samme funksjonene kan realiseres i en sannhetstabell(også kalt funksjonstabell). For å indikere logisk høy og lav benytter vi de binære verdiene 1 og 0. I datablad for integrerte logiske kretser benyttes ofte også H (High/høy) og L (Low/lav).
EX står for eksklusiv, det vil si eksklusiv ELLER og eksklusiv NELLER.
Oversikt logiske porter, tegningssymboler og sannhetstabeller
Europeiske og amerikanske tegningssymboler. Datablader benytter vanligvis amerikanske symboler.
Her er kun tatt med porter med to innganger. Det finnes portkretser som også har flere innganger, men de er ikke tatt med her.
Legg merke til spesialsymbolet som kan brukes for å markere eksklusiv ELLER.
Integrert krets
Eksempel på integrert krets bestående av fire ELLER-porter med tilhørende nummer for pinnetilkobling samt tilkobling for jord (GND) og driftsspenning (VCC).
Som vi ser, har denne komponenten til sammen 14 tilkoblingsbein fordelt på to rader. Komponenter i denne utførelsen kalles DIL-komponenter (Dual In Line).
Digitale integrerte kretser bygges vanligvis inn i en rektangulær brikke av keramikk eller plast.
Vi skiller mellom
hullmonterte kretser
overflatemonterte kretser
Ved hullmontering stikkes beina gjennom kretskortet og loddes fast. Ved overflatemontering loddes/limes beina fast til kortets overflate. Selve den elektroniske kretsen er etset inn på en ørliten silisiumskive med komponenter og ledningsforbindelser.
Logiske nett, boolsk algebra og karnaughdiagram
Oppgaver digitale kretser
Reduser de logiske uttrykkene a) og b) ved hjelp av forenklingsregler og c) og d) ved hjelp av Karnaughdiagram:
Oppgave
Sett opp det logiske uttrykket for X og gjør uttrykket så enkelt som mulig.
Fyll ut sannhetstabellen for den logiske kretsen.
Fullfør sekvensdiagrammet.
Hvis du har komponenter og utstyr tilgjengelig, TTL eller CMOS, finn frem aktuelle komponenter og koble kretsen opp på en digital trainer.
Test ut kretsen ved å legge signaler på inngangene og måle på utgangen ved hjelp av oscilloskop. Kontroller at resultatet stemmer med det du har satt inn i funksjonstabellen.
Har du tilgang til tegne- og simuleringsprogrammet Multisim, kan du også tegne og simulere kretsen der.
Oppgave
Boksen på tegningen har en funksjon gitt ut fra viste sannhetstabell.
Sett opp det logiske uttrykket for X ut fra sannhetstabellen.
Tegn kretsen som boksen inneholder, ut fra det logiske uttrykket.